Shields Formula

The Shields formula is a formula for the stability calculation of granular material (sand, gravel) in running water.

The stability of granular material in flow can be determined by the Shields formula or the Izbash formula. The first is more suitable for fine grain material (such as sand and gravel), while the Izbash formula is more suitable for larger stone. The Shields formula was developed by Albert F. Shields (1908-1974). In fact, the Shields method determines whether or not the soil material will move. The Shields parameter thus determines whether or not there is a beginning of movement.

Derivation

Movement of (loose grained) soil material occurs when the shear pressure exerted by the water on the soil is greater than the resistance the soil provides. This dimensionless ratio (the Shields parameter) was first described by Albert Shields and reads:
:$\Psi_c*=\frac = \frac$,

in which is
* $\tau_c$ the critical bottom shear stress;
* $\rho_s$ is density of sediment;
* $\rho_w$ is the density of water;
* $g$ is the acceleration of gravity;
* $d$ is the diameter of the sediment.

The shear stress that works on the bottom (with a normal uniform flow along a slope) is:

:$\tau=\rho_w g h I$

In which is
* $\tau$ the shear tension exerted by the flow on the bed;
* $h$ is the water depth;
* $I$ is the gradient (= the slope of the current).

Important to realise is that $\tau$ is the shear stress exerted by the flow (i.e. a property of the flow) and $\tau_c$ shear stress at which the grains move (i.e. a property of the grains).

The shear stress velocity is often used instead of the shear stress:
:$u_* =\sqrt$

The shear stress velocity has the dimension of a velocity (m/s), but is actually a representation of the shear stress. So the shear stress velocity can never be measured with a velocity meter.

By using the shear stress velocity, the Shields parameter can also be written as:
:$\Psi_= \frac = \frac$

where:
* $\Delta$ is the dimensionless grainsize $\frac$

Shields found that the parameter $\Psi_$ is a function of $\frac$, in which $\nu$ is the kinematic viscosity. This parameter is also called the granular reynolds number:
:$Re_* = \frac$

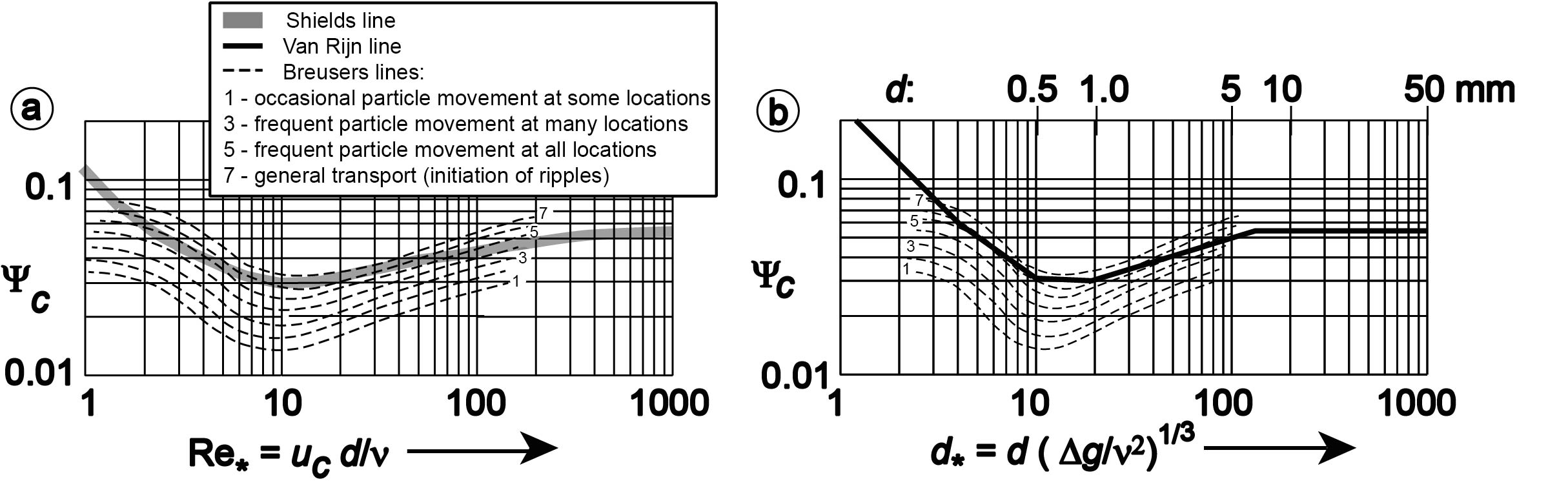
Shields has performed tests with grains of different densities, and the found value of $\Psi_$ plotted as a function of $Re_*$. This led to the above graph.

Van Rijn found that instead of the granular reynolds number a dimensionless grain size could be used:
:$= d ^$
Because usually the values of $\Delta, g, \nu$ are quite constant, the true grain size can also be set on the horizontal axis (see right figure b). This means that the value of $\Psi_$ is only a function of the grain diameter and can be read directly.

.

From this follows that for grains greater than 5 mm the Shields parameter gets a constant value of 0,055.

The gradient of a river (''I'') can be determined by Chézy formula:
:$u= C \sqrt$
in which $C$ = the coefficiënt of Chézy (m^½/s); This is often in the order 50 (m½/s). For a flat bed (i.e. without ripples) C can be approximated with:
:$C=18 \log _$

By introducing this into the stability formula, a critical grain size formula is found at a given flow rate:
:$d_c=\frac$
In this form, the stability relationship is usually called the “Shields formula”.

Definition of "incipient motion"

The line of Shields (and of Van Rijn) in the graph is the separation between “movement” and “no movement”. Shields has defined as “movement” that almost all grains move on the bottom. This is a useful definition for defining the beginning of sand transport by flow. However, if one wants to protect a bed from erosion, the requirement is that grains should hardly move. To make this operational, Breusers defined 7 phases of movement in 1969:

# Every now and then a moving stone
# Frequent movement in some places
# Frequent movement in several places
# Frequent movement in many places
# Continuous movement at all points
# Transport of all grains at the bottom

These phases are shown in the figure below:

Visually, these phases are also shown in a series of short video clips. In these video fragments, “no” is the Shields parameter used.

In practice, this means that for bed protections (where the grain is always larger than 5mm), a design value of Ψ=0.03 must be used.

Calculation Example

Question: At what speed of flow does sand of 0.2cm move at a water depth of 1m?
:The Chézy value then becomes ''C'' = 62 (this is a high value, so a smooth soil; This is because we assume there are no ridges). Filled in this gives a speed of 0.83 m/s.

Question: What stone size is needed to defend this soil against a current of 2 m/s?
:This cannot be solved directly, first an assumption must be made for the ''d''. Take a stone size of 5cm. That gives a Chézy value of 37. When this is entered in the Shields formula it gives a stone size of 5.7cm. The 5cm was a little too small. By trying, a stone size of 6.5cm is finally found. (In this case, Izbash’s formula gives 6.3cm)

Restrictions

The Shields approach is based on a uniform, permanent flow with a turbulence generated by the bed roughness (i.e. no additional turbulence by a for example a propeller current). In the case of a rough bed in shallow water, and in case of unusual turbulence, the Izbash's formula is therefore more recommended.

References

{{Reflist

Hydrology
Geomorphology
Curves
Rivers
Sedimentology